Penerapan FSA,DFA(Deterministik Finite Automata),NFA( Non deterministik finite automata) ekuivalen atar DFA,Reduksi jumlah state

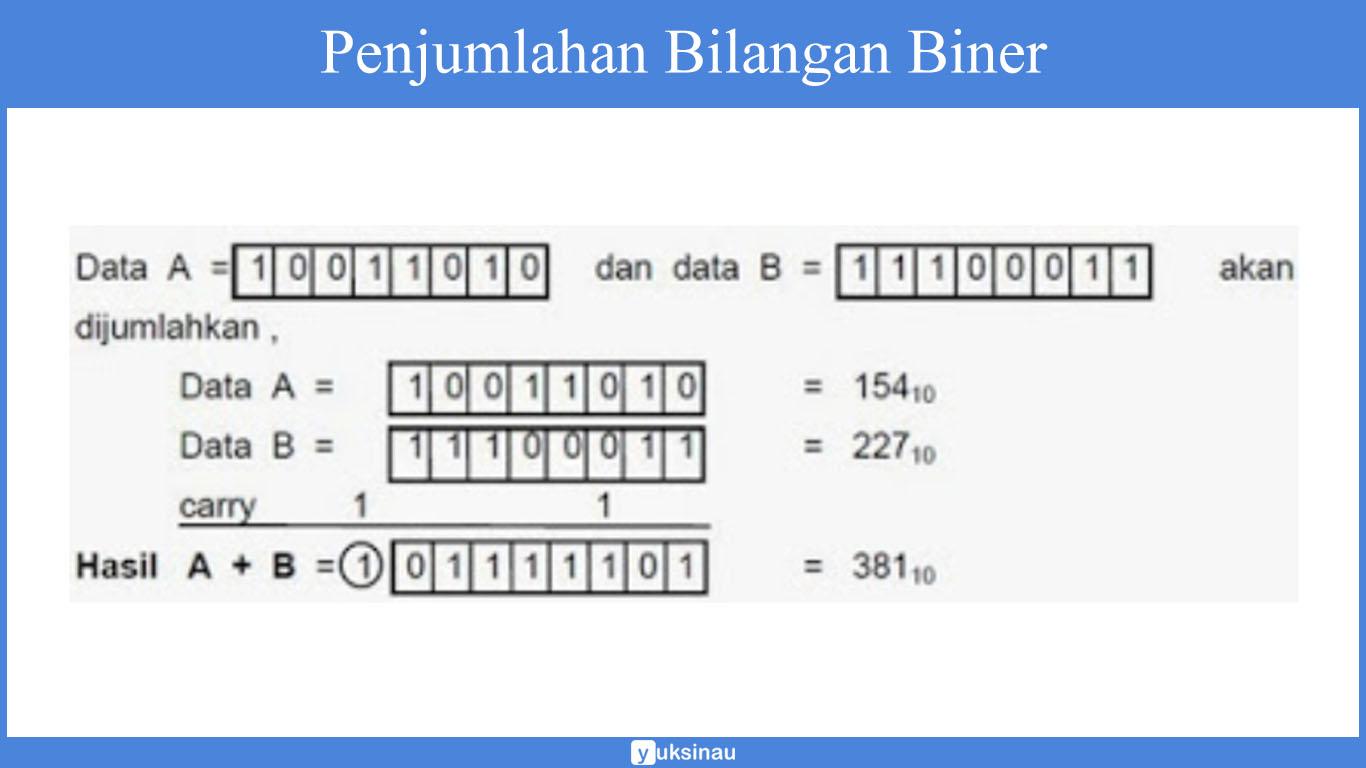
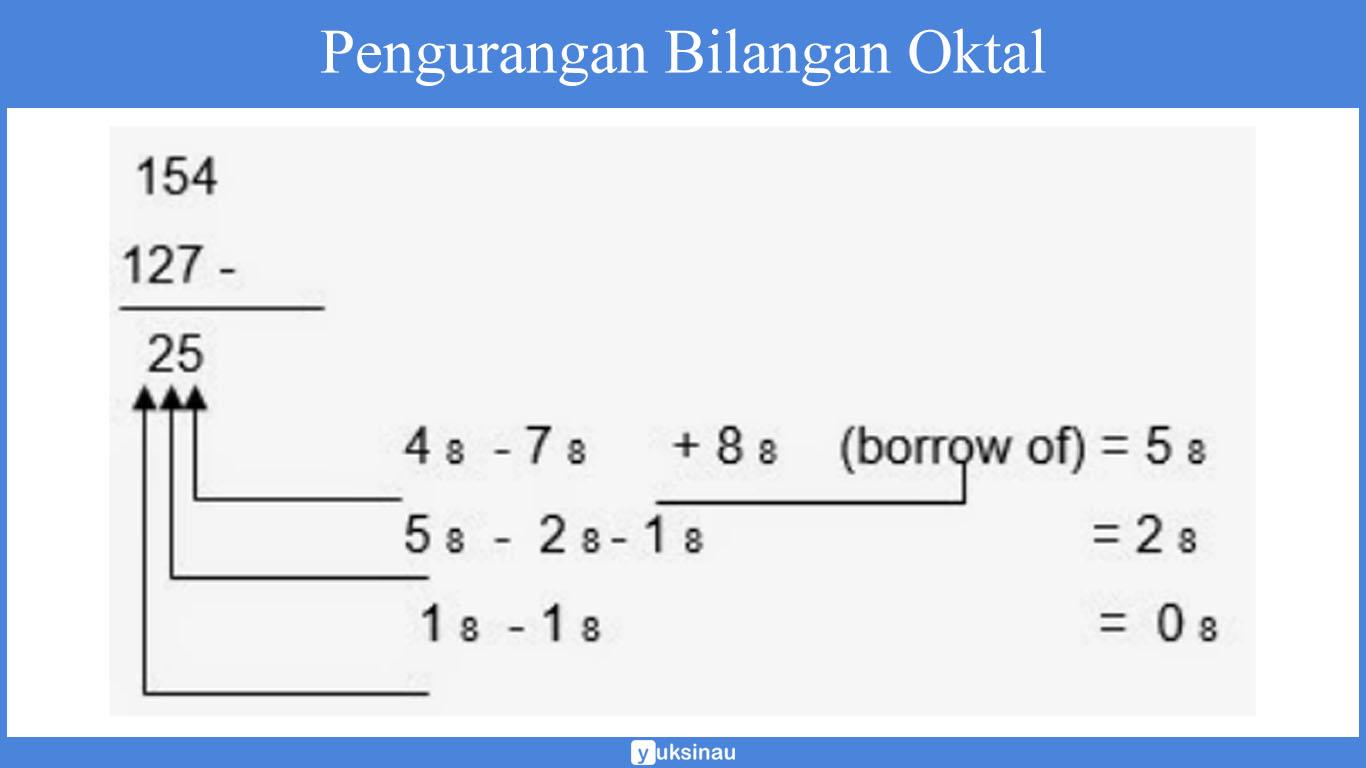
1. Penerapan FSA

Finite state automata adalah mesin abstrak berupa sistem model matematika dengan masukan dan keluaran diskrit yang dapat mengenali bahasa paling sederhana (bahasa reguler) dan dapat diimplementasikan secara nyata.

Finite State Automata (FSA) adalah model matematika yang dapat menerima input dan mengeluarkan output yang memiliki state yang berhingga banyaknya dan dapat berpindah dari satu state ke state lainnya berdasarkan input dan fungsi transisi. Finite state automata tidak memiliki tempat penyimpanan/memory, hanya bisa mengingat state terkini.

Finite State Automata dinyatakan oleh pasangan 5 tuple, yaitu:
M=(Q , Σ , δ , S , F )
Q = himpunan state
Σ = himpunan simbol input
δ = fungsi transisi δ : Q × Σ
S = state awal / initial state , S ∈ Q
F = state akhir, F ⊆ Q

Karakteristik Finite Automata :

1.Setiap Finite Automata memiliki keadaan dan transisi yang terbatas.
2.Transisi dari satu keadaan ke keadaan lainnya dapat bersifat deterministik atau non-deterministik.
3.Setiap Finite Automata selalu memiliki keadaan awal.
4.Finite Automata dapat memiliki lebih dari satu keadaan akhir.
jika setelah pemrosesan seluruh string, keadaan akhir dicapai, artinya otomata menerima string tersebut.

Setiap FSA memiliki:

1.Himpunan berhingga (finite) status (state)
•Satu buah status sebagai status awal (initial state), biasa dinyatakan q0.
•Beberapa buah status sebagai status akhir (final state).
2.Himpunan berhingga simbol masukan
3.Fungsi transisi
Menentukan status berikutnya dari setiap pasang status dan sebuah simbol masukan.

Cara Kerja Finite State Automata

Finite State Automata bekerja dengan cara mesin membaca memori masukan berupa tape yaitu 1 karakter tiap saat (dari kiri ke kanan) menggunakan head baca yang dikendalikan oleh kotak kendali state berhingga dimana pada mesin terdapat sejumlah state berhingga.

Finite Automata selalu dalam kondisi yang disebut state awal (initial state) pada saat Finite Automata mulai membaca tape. Perubahan state terjadi pada mesin ketika sebuah karakter berikutnya dibaca. Ketika head telah sampai pada akhir tape dan kondisi yang ditemui adalah state akhir, maka string yang terdapat pada tape dikatakan diterima Finite Automata (String-string merupakan milik bahasa bila diterima Finite Automata bahasa tersebut).

contoh :

seorang  petani dengan seekor serigala ,kambing dan seikat rumput berada pada suatu sisi sungai.

tersedia hanya sebuah perahu kecil yang hanya dapat dimuati dengan petani tersebut dengan salah satu serigala,kambing atau rumput.

petani tersebut harus menyebrangkan ketiga bawaanya kesisi lain sungai .

tetapi jika petani meninggalkan serigala dan kambing pada suatu saat ,maka kambing akan dimakan serigala .

begitu pula jika kambing ditinggal dengan rumput ,maka rumput akan dimakan oleh kambing .

mungkinkah ditemukan suatu cara untuk melintasi sungai tanpa menyebabkan kambing atau rumput dimakan.

16 kemungkinan kombinasi state

 Diagram Transisi 

2.DFA

dari suatu state ada tepat satu state berikutnya untuk setiap simbol masukan yang diterima. Deterministik artinya tertentu/sudah tertentu fungsi transisinya.

Notasi matematis DFA:

• M = nama DFA

• Q = himpunan keadaan DFA

• S = himpunan alfabet

• d = fungsi transisi

• q0 = keadaan awal

• F = keadaan akhir

M = (Q, S, d, q0, F)

Contoh : Pengujian untuk menerima bit string dengan banyaknya 0 genap, serta banyaknya 1 genap.

0011 : diterima

10010 : ditolak, karena banyaknya 0 ganjil

Diagram transisi-nya :

DFA nya:

Q = {q0 , q1 , q2 , q3 }

Σ = {0,1}

S = q0

F = { q0}

δ( q0,011)= δ( q2,11) =δ( q3,1)= q2  Ditolak

δ( q0,1010)= δ( q1,010) =δ( q3,10)=δ( q2,0)= q0 Diterima

3.NFA (Non deterministik finite automata)

dari suatu state ada 0, 1 atau lebih state    berikutnya untuk setiap simbol masukan yang diterima.

Non-Deterministic Finite Automata:

•  Otomata berhingga yang tidak pasti untuk setiap pasangan state input, bisa memiliki 0 (nol) atau lebih pilihan untuk state berikutnya.
•  Untuk setiap state tidak selalu tepat ada satu state berikutnya untuk setiap simbol input yang ada.
• Dari suatu state bisa terdapat 0,1 atau lebih busur keluar (transisi) berlabel simbol input yang sama.
• Untuk NFA harus dicoba semua kemungkinan yang ada sampai terdapat satu yang mencapai state akhir.
• Suatu string x dinyatakan diterima oleh bahasa NFA, M= (Q, _, d, S, F) bila {x | d (S,x) memuat sebuah state di dalam F}

Kedua finite automata di atas mampu mengenali himpunan reguler secara presisi. Dengan demikian kedua finite automata itu dapat mengenali string-string yang ditunjukkan dengan ekspresi reguler secara tepat.

DFA dapat menuntun recognizer(pengenal) lebih cepat dibanding NDFA. Namun demikian, DFA berukuran lebih besar dibanding NDFA yang ekivalen dengannya. Lebih mudah membangun NDFA dibanding DFA untuk suatu bahasa, namun lebih mudah mengimplementasikan DFA dibanding NDFA.

4 .Ekuivalen antar DFA

Untuk suatu bahasa regular, kemungkinan ada sejumlah Deterministic Finite Automata yang dapat menerimanya. Perbedaannya hanyalah jumlah state yang dimiliki otomata-otomata yang saling ekuivalen tersebut. Tentu saja, dengan alasan kepraktisan, kita memilih otomata dengan jumlah state yang lebih sedikit.

Sasaran kita di sini adalah mengurangi jumlah state dari suatu Finite State Automata, dengan tidak mengurangi kemampuannya semula untuk menerima suatu bahasa.

Ada dua buah istilah baru yang perlu kita ketahui yaitu :

1. Distinguishable yang berarti dapat dibedakan.

2. Indistinguishable yang berarti tidak dapat dibedakan.

Dua DFA M1 dan M2 dinyatakan ekivalen apabila L(M1) = L(M2)

5. Reduksi jumlah state

Reduksi Jumlah State Pada FSA

Reduksi dilakukan untuk mengurangi jumlah state tanpa mengurangi kemampuan untuk menerima suatu bahasa seperti semula (efisiensi). State pada FSA dapat direduksi apabila terdapat useless state. Hasil dari FSA yang direduksi merupakan ekivalensi dari FSA semula

Pasangan State dapat dikelompokkan berdasarkan:

1. Distinguishable State (dapat dibedakan)

    Dua state  p dan q dari suatu DFA dikatakan indistinguishable apabila:

                δ(q,w) Î F dan  δ(p,w) Î F   atau   δ(q,w) ∉ F dan  δ(p,w) ∉ F

                untuk semua w Î S*

2. Indistinguishable State ( tidak dapat dibedakan)

    Dua state  p dan q dari suatu DFA dikatakan distinguishable jika ada string w Î S*  hingga:

                                                  δ(q,w) Î F dan  δ(p,w) ∉ F

Reduksi Jumlah State Pada FSA – Relasi

Pasangan dua buah state memiliki salah satu kemungkinan : distinguishable atau indistinguishable tetapi tidak kedua-duanya. 

Dalam hal ini terdapat sebuah relasi :

Jika         p dan q    indistinguishable,

dan         q  dan r    indistinguishable

maka      p,  r          indistinguishable 

dan         p,q,r         indistinguishable

Dalam melakukan eveluasi state, didefinisikan suatu relasi :

     Untuk Q yg merupakan himpunan semua state

• D  adalah  himpunan state-state distinguishable,  dimana D Ì Q
• N  adalah himpunan state-state indistinguishable, dimana N Ì Q
• maka     x Î N  jika  x Î Q  dan x ∉  D

Reduksi Jumlah State Pada FSA – Step

Langkah - langkah untuk melakukan reduksi ini adalah :

1. Hapuslah semua state yg tidak dapat dicapai dari state awal  (useless state)
2. Buatlah semua pasangan state (p, q) yang distinguishable, dimana p Π F dan q ∉ F. Catat semua pasangan-pasangan state tersebut.
3. Cari state lain yang distinguishable dengan aturan:                                                              Untuk semua (p, q) dan semua a Î ∑, hitunglah  δ (p, a) = pa dan δ (q, a) = qa  . Jika pasangan (pa, qa) adalah pasangan state yang distinguishable maka pasangan (p, q) juga termasuk pasangan yang distinguishable.
4. Semua pasangan state yang tidak termasuk sebagai state yang distinguishable merupakan state-state indistinguishable.
5. Beberapa state yang indistinguishable dapat digabungkan menjadi satu state.

  Sesuaikan transisi dari state-state gabungan tersebut.

1. State  q5 tidak dapat dicapai dari state awal dengan jalan apapun (useless state).  Hapus state q5

2. Catat state-state distinguishable, yaitu :                                                                                    

q4 Î F sedang q0, q1, q2, q3 ∉ F sehingga pasangan                                                              

(q0, q4) (q1, q4) (q2, q4) dan (q3, q4) adalah distinguishable.

3. Pasangan-pasangan state lain yang distinguishable diturunkan berdasarkan pasangan dari langkah 2, yaitu :                                                                                                                                

Untuk pasangan (q0, q1)                                                                                                      

          δ(q0, 0) = q1   dan   δ(q1, 0) = q2   à  belum teridentifikasi                                                                     δ(q0, 1) = q3   dan   δ(q1, 1) = q4   à  (q3, q4) distinguishable   

          maka         (q0, q1) adalah distinguishable.                                                                                               

Untuk pasangan (q0, q2)

          δ(q0, 0) = q1   dan   δ(q2, 0) = q1   à  belum teridentifikasi 

          δ(q0, 1) = q3   dan   δ(q2, 1) = q4   à  (q3, q4) distinguishable                     

          maka         (q0, q2) adalah distinguishable.

4. Setelah diperiksa semua pasangan state  maka terdapat state-state yang distinguishable : (q0,q1), (q0,q2), (q0,q3),  (q0,q4), (q1,q4),  (q2,q4), (q3,q4). Karena berdasarkan relasi-relasi yang ada, tidak dapat dibuktikan (q1, q2), (q1, q3) dan (q2, q3) distinguishable,  sehingga disimpulkan pasangan-pasangan state tersebut indistinguishable.

5. Karena q1 indistinguishable dengan q2,  q2 indistinguishable dengan q3, maka dapat disimpulkan q1, q2, q3 saling indistinguishable dan dapat dijadikan satu state.

6. Berdasarkan hasil diatas  maka hasil dari DFA yang direduksi menjadi:

daftar pustaka:
https://hennyhalimah.blogspot.com/2017/07/ekuivalensi-antar-deterministic-finite.html

http://dhiyakhai.blogspot.com/2018/06/ekuivalensi-antar-deterministic-finite.html

https://riskasimaremare.wordpress.com/2013/04/23/finite-state-automata/

tujuan penyederhanaan arsitektur komputer

Tujuan penyederhanaan

melakukan pembatasan sehingga tidak menghasilkan pohon penurunan yang memiliki kerumitan yang tak perlu atau aturan produksi yang didak berarti .

suatu tata bahasa bebas konteks dapat disederhanakan dengan melakukan cara berikut ini:

1. penghilang produksi useless

2. penghilang produksi unit 

3. penghilang Produksi ε 

Penghilang produksi useless

produksi useless adalah :

• produksi yang membuat simbol variabel yang tidak  memiliki penurunan yang akan menghassila terminal-terminal seluruhnya (masih ada simbol variabel yang tersisa)
• produksi yang tidak akan pernah dicapai dengan penurunan apapun dari simbol awal sehingga produksi itu redudan (berlebih). 

contoh :

soal:

S > aB | C                     B > aB

B > e |Ab                     C > ab

C > bCb | adF | ab       

F > cFB

jawab:

S > Aa | B        S > Ab | B

A > ab | D        A > ab

B > b | E           B > b

C > bb

E > aEa 

dapat disimpulkan :

1. C adalah redudan
2. konsekuensi dari no.1,

penjumlahan bilangan desimal positif dengan negatif dan penjumlahan biner positif dengan negatif

PENJUMLAHAN BILANGAN DESIMAL POSITIF DENGAN NEGATIF 

pada penjumlahan bilangan positif dan negatif bilangan desimal sama seperti penjummlahan bilangan positif dan negatif pada umumnya .


1. 5 - 4 =  1
2. -7 + 2 = -5

PENJUMLAHAN BILANGAN BINER POSITIF DENGAN NEGATIF

lalu dikonverikan ke biner dan ketentuan penjumlahanya seperti di bawah:

mengkonversi  desimal ke biner bilangan positif:

contoh

32 16 8 4 1 adalah rumus konversi desimal ke biner
contoh kita mengkonversi 5 desimal ke 5 biner maka dari rumus konversi berapa dijumlah dengan berapa sehingga hasilnya 5 

32 16 8 4 2 1
          0 1 0 1 = 5

dari rumus konversi 5 adalah desimal dari 4 + 1 maka 1 dan 4 kita beri nilai 1 dan selainya adalah 0
jika di perkecil lagi menjadi seperti ini :

8 4 2 1
0 1 0 1 = 5

begitu juga contoh di bawah :

32 16 8 4 2 1
          0 0 1 0 = 2
untuk mengkonversi bilangan desimal ke  biner negatif :

caranya adalah dengan menulis kebalikan dari biner positif .

contoh : 0101 =  5
maka     1010 = -5

ketentuan penjumlahan bilangan biner negatif dengan positif :


Komputer atau mesin digital akan bekerja menggunakan sistem biner. Oleh karena itu pemahaman bilangan biner adalah sesuatu yang sangat penting dalam memahami sistem digital.

Sebagaimana bilangan pada umumnya, di dalam sistem biner juga mengenal bilangan negatif maupun posistif. Bagaimanakah hal ini dilakukan di dalam sistem biner?? Ada beberapa cara, antara lain:

1. Label tanda konvensional : + dan –
Contoh : +4 dan -4

2. Menggunakan posisi digit sebelah kiri (MSB) sebagai sign digit (0 untuk
positif dan 1 untuk negatif).
Contoh :Sign-Magnitude –4 dalam 4 bit = 1100
Magnitude dari bilangan positif dan negatif sama hanya berbeda pada sign
digitnya/MSB.

3. Representasi Komplemen-1
Angka nol diubah menjadi satu dan satu menjadi nol.
Contoh : Dalam 4 bit +1 = 0001, -1 = 1110

4. Representasi Komplemen-2
Dengan representasi komplemen-1 ditambah 1.
Contoh : Dalam 4 bit -1 = 1110 (Komplemen-1) + 1 = 1111
contoh menggunakan 4 bit :

posotif (+)                                                                       negatif (-)  di komplemen

1 = 0001                                                                          -1 = 1110 +1 = 1111
2 = 0010                                                                          -2 = 1101 +1 = 1110
3 = 0011                                                                          -3 = 1100 +1 = 1101
4 = 0100                                                                          -4 = 1011 +1 = 1100
5 = 0101                                                                          -5 = 1010 +1 = 1011
6 = 0110                                                                          -6 = 1001 +1 = 1010
7 = 0111                                                                          -7 = 0110 +1 = 1001


lalu kita jumlahkan soal desimal diatas :
soal 1.
       1
 5 = 0101
-4 = 1100
       _____ +
       10001
karna kita menggunakan 4 bit maka angka 1 di depan di hapus sehingga hasilnya 0001 = 1
maka hasilnya benar 5 - 2 = 1

lalu lanjut ke soal nomor 2 yaitu -7 + 2 = 5

soal 2.

-7 = 1001
 2 = 0010
      ______+
       1011 = -5
maka jawabanya benar -7 + 2 = -5



daftar pustaka :

https://fatchul-uny.blogspot.com/2010/03/representasi-positif-dan-negatif.html

bilangan desimal,biner,okta dan hexa

MACAM - MACAM  BILANGAN

• Bilangan biner (Bilangan berbasis dua, bilangannya: 0,1)
• Bilangan octal (Bilangan berbasis delapan bilangannya: 0,1,2,3,4,5,6,7)
• Bilangan desimal (Bilangan berbasis sepuluh, bilangannya: 0,1,2,3,4,5,6,7,8,9)
• Bilangan hexadesimal (Bilangan berbasis enam belas, bilangannya: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F)

KONVERSI BILANGANYA

Bilangan Biner ke Oktal
yaitu dengan cara mengambil 3 karakter dari kanan, setelah itu cocokkan dengan angka pada tabel diatas. Jika angka terakhir kurang dari 3 karakter, maka bisa ditambahkan angka 0 di kiri angka untuk memudahkan pengoperasian.

contoh:
11110111001(2) = . . .(8)
011  110  111  001
3      6      7     1
jadi, 11110111001(2) = 3671(8)

Bilangan Biner ke Hexa Decimal
yaitu dengan cara mengambil 4 karakter dari kanan. kemudian cocokkan dengan angka pada tabel diatas. Jika angka terakhir kurang dari 4 karakter, maka bisa ditambahkan angka 0 untuk memudahkan pengoperasian.  Contoh:
1110111111010100(2) = . . . (16)
1110 1111 1101 0100
14     15     13    4
E       F      D    4
jadi, 1110111111010100(2) = EFD4(16)

Bilangan Oktal ke Biner
yaitu dengan cara menterjemahkan angka oktal kedalam angka biner melalui tabel biner di atas.
contoh:
4573(8) = . . . (2)
4     5    7    3
100 101 111 011
jadi, 4573(8) = 100101111011(2)

Bilangan Oktal ke Hexa
yaitu dengan cara menterjemahkan ke angka biner melalui tabel, kemudian dari angka biner baru terjemahkan ke angka hexa decimal dengan cara mengambil 4 karakter dari angka biner tersebut.
contoh:
756(8) = . . . (16)
7     5    6
111 101 110
111101110(2)
0001 1110 1110
1        14     14
1         E      E
jadi, 756(8) = 1EE(16)

Bilangan Hexa decimal ke biner
yaitu dengan cara menterjemahkan angka hexa kedalam biner melaui tabel di atas.
contoh:
ADE(16) = . . . (2)
A     D      E
1010 1101 1110
jadi, ADE(16) = 101011011110(2)

Bilangan Hexa decimal ke Oktal
yaitu dengan cara menterjemahkan angka hexa decimal ke dalam biner melalui tabel, kemudian diterjemahkan lagi ke dalam bentuk Oktal dengan cara mengambil 3 karakter dari kanan, setelah itu cocokkan dengan angka pada tabel diatas. Jika angka terakhir kurang dari 3 karakter, maka bisa ditambahkan angka 0 di kiri angka untuk memudahkan pengoperasian.
contoh:
F1(16) = . . . (2)
F      1
1111 0001
11110001(2)
011 110 001
3     6    1

1. Operasi Aritmatika Bilangan Biner

Aritmatika Bilangan Binner merupakan beberapa operasi perhitungan yang terjadi dalam bilangan biner.

Terdapat 5 operasi aritmatika pada bilangan biner, antara lain:

1. Penjumlahan
2. Pengurangan
3. Perkalian
4. Pembagian
5. Bilangan Biner Bertanda

A. Penjumlahan Bilangan Biner

Dalam bilangan biner terdapat dua aturan dasar, antara lain:

0 + 0 = 0
1 + 0 = 1
0 + 1 = 1
1 + 1 = 1, simpan 1

Sebagai cara penjumlahan bilangan desimal yang kalian kenal sehari-hari, penjumlahan bilangan biner juga harus selalu memperhatikan carry (sisa) dari hasil penjumlahan pada tempat yang lebih rendah.

Sebagai contoh:

Soal 1.

1111 2
10100 2
_______+
100011 2 Carry of 1 (3 kali)

Soal 2.

Dalam contoh diatas, telah dilakukan penjumlahan 8 bit tanpa carry, sehingga hasil penjumlahnya masih berupa 8 bit data. Untuk contoh berikutnya akan dilakukan penjumlahan 8 bityang menghasilkan carry.

Soal 3.

Hasil penjumlahan diatas menjadi 9 bit data, sehingga untuk 8 bit data, hasil penjumlahannya bukan merupakan jumlah 8 bit data A dan B tetapi bit yang e-8 (dihitung mulai dari 0) atau yang disebut carry juga harus diperhatikan  sebagai hasil penjumlahan.

B. Pengurangan Bilangan Biner

Pada bilangan biner terdapat dua cara dalam pengurangan yakni dengan 1s complement dan 2s complement, Perbedaan diantara keduanya antara lain:

• 1s complement
  merupakan sebuah cara untuk membalikkan bilangan negatif menjadi positif (sebab sebenarnya dalam bahasa komputer tidak kenal operasi pengurangan).
  Sehingga operasi pengurangan ini akan menjadi penjumlahan.
  1s complement dari sebuah bilangan dilakukan dengan mengubah 0 menjadi 1 dan 1 menjadi 0. Sebagai contoh: 
• 2s complement kurang lebih mempunyai fungsi yang sama dengan 1s complement yakin membuat sebuah bilangan negatif menjadi positif. Tetapi cara 2s complement sedikit ada perbedaan yakni 1s complement yang ditambah dengan 1. Sebagai contoh:  
  Sehingga 2s complement dari 10001 yaitu 01111 dan 1s complement-nya yaitu 01110.

C. Perkalian Bilangan Biner

Dilakukan sama dengan cara perkalian yang terdapat dalam operasi bilangan desimal. Dasar perkalian pada bilangan biner ialah sebagai berikut:

0 x 0 = 0
1 x 0 = 0
0 x 1 = 0
1 x 1 = 1

Sebagai contoh:

Soal 1.

1110 2

           1100 2 x

           0000

         0000

        1110

      1110 +

      10101000 2

D. Pembagian Bilangan Biner

Pembagian biner dilaksanakan dengan menggunakan cara yang sama dengan yang ada pada bilangan desimal. Pembagian biner 0 tidak memiliki arti, sehingga dasar pembagian pada bilangan biner adalah sebagai berikut:

0 : 1 = 0

1 : 1 = 1

Contoh #1:

101 / 1111101 \ 11001

        101 _

         101

         101 _

          0101

            101 _

              0

2.Operasi Aritmatika Bilangan Oktal

A. Penjumlahan Bilangan Oktal

Berikut adalah tahapan untuk operasi penjumlahan oktal, antara lain:

1. tambahkan masing-masing kolom secara desimal
2. rubah dari hasil desimal ke dalam bilangan oktal
3. tuliskan hasil dari digit paling kanan dari hasil oktal
4. jika hasil penjumlahan pada masing-masing kolom terdiri dari dua digit, maka digit paling kiri adalah carry of untuk penjumlahan kolom berikutnya.
5. sisa akan muncul atau terjadi apabila jumlahnya sudah melebihi 7 pada setiap tempat.

Sebagai contoh:

B. Pengurangan Bilangan Oktal

Pengurangan Oktal bisa dilakukan dengan cara yang sama dengan yang ada pada operasi pengurangan bilangan desimal.

Pada pengurangan apabila bilangan yang dikurangi lebih kecil dari pada bilangan pengurangnya maka akan dilakukan peminjaman (borrow) pada tempat yang lebih tinggi (dengan nilai 8).

Sebagai contoh:

C. Perkalian Bilangan Oktal

Berikut adalah tahapan untuk operasi perkalian oktal, antara lain:

1. kalikan masing-masing kolom secara desimal.
2. rubah dari hasil desimal ke bilagan oktal.
3. tuliskan hasil dari digit paling kanan dari hasil oktal.
4. jika hasil perkalian pada masing-masing kolom terdiri atas 2 digit, maka digit paling kiri adalah carry of untuk ditambahkan pada hasil perkalian pada kolom berikutnya.

D. Pembagian Bilang Oktal

3. Operasi Aritmatika Bilangan Heksadesimal

A. Penjumlahan Bilangan Heksadesimal

Dalam penjumlahan bilangan heksadesimal, sisa akan terjadi atau berlangsung apabila jumlah dari masing-masing tempat melebihi 15.

Sebagai contoh:

B. Pengurangan Bilangan Heksadesimal

Pada pengurangan apabila bilangan yang dikurangi lebih kecil dibandingkan dengan bilangan pengurangnya maka akandilakukan peminjaman (borrow) pada tempat yang lebih tinggi (dengan nilai 16).

Sebagai contoh:

C. Perkalian Bilangan Heksadesimal

Berikut adalah tahapan untuk operasi perkalian heksadesimal, antara lain:

1. kalikan masing-masing kolom secara
2. rubah dari hasil desimal ke oktal
3. tuliskan hasil dari digit paling kanan dari hasil bilangan oktal
4. jika hasil perkalian pada masing-masing kolom terdiri atas 2 digit, maka digit paling kiri adalah carry of untuk ditambahkan pada hasil perkalian kolom berikutnya.

Sebagai contoh:

D. Pembagian Bilangan Heksadesimal

Pembagian pada bilangan Heksadesimal sama halnya seperti yang ada dalam pembagian pada bilangan decimal.

Sebagai contoh:

Increment dan Decrement

Increment (bertambah) dan Decrement (berkurang) merupakan dua pengertian yang sering sekali dipakai dalam teknik miroprosessor.

Dalam matematik pengertian increment yaitu Bertambah Satu dan decrement berarti Berkurang Satu.

Increment Sistem Bilangan

Seperti uraian di atas bahwa increment berarti bilangan sebelumnya akan ditambah dengan 1.

Decrement Sistem Bilangan

Decrement didapatkan dengan cara mengurangi bilangan sebelumnya dengan 1.

Sebagai contoh:

4.bilangan desimal

Tabel Konversi

bilangan desimal adalah bilangan berbasis 10 terdiri dari kombinasi angka 0 s.d. 9, bilangan ini paling umum dijumpai dan dijadikan sebagai bilangan yang umum digunakan pada software yang berinteraksi langsung dengan manusia.

aritmatika bilangan desimal

pada perhitungan aritmatika bilangan disini sama seperti perhitungan pada umumnya 

a. penjumlahan

misalnya:

123

356

_____ +

479

b. pengurangan

479

123

____ +

356

c. perkalian

25

10

___ x

00

25

______ +

250

daftar pustaka :

https://www.yuksinau.id/operasi-aritmatika/

https://blogs.itb.ac.id/ku1071k0316213103nurhidayatf/2013/11/15/cara-mengkonversi-bilangan-biner-hexa-desimal/

https://desylvia.wordpress.com/2010/09/21/bilangan-desimal-biner-hexa-octal/

https://desylvia.wordpress.com/2010/09/21/bilangan-desimal-biner-hexa-octal/